_images/ChASE_Logo_RGB.png

ChASE: an Iterative Solver for Dense Eigenproblems

Overview

The Chebyshev Accelerated Subspace Eigensolver (ChASE) is a modern and scalable library to solve dense Hermitian (Symmetric) algebraic eigenvalue problems of the form

\[A \hat{x} = \lambda \hat{x} \quad \textrm{with} \quad A^\dagger=A \in \mathbb{C}^{n\times n}\ \ (A^T=A \in \mathbb{R}^{n\times n}),\]

where \(\hat{x} \in \mathbb{C}^{n}\backslash \{0\}\) and \(\lambda \in \mathbb{R}\) are the eigenvector and the eigenvalue of \(A\), respectively.

Algorithm

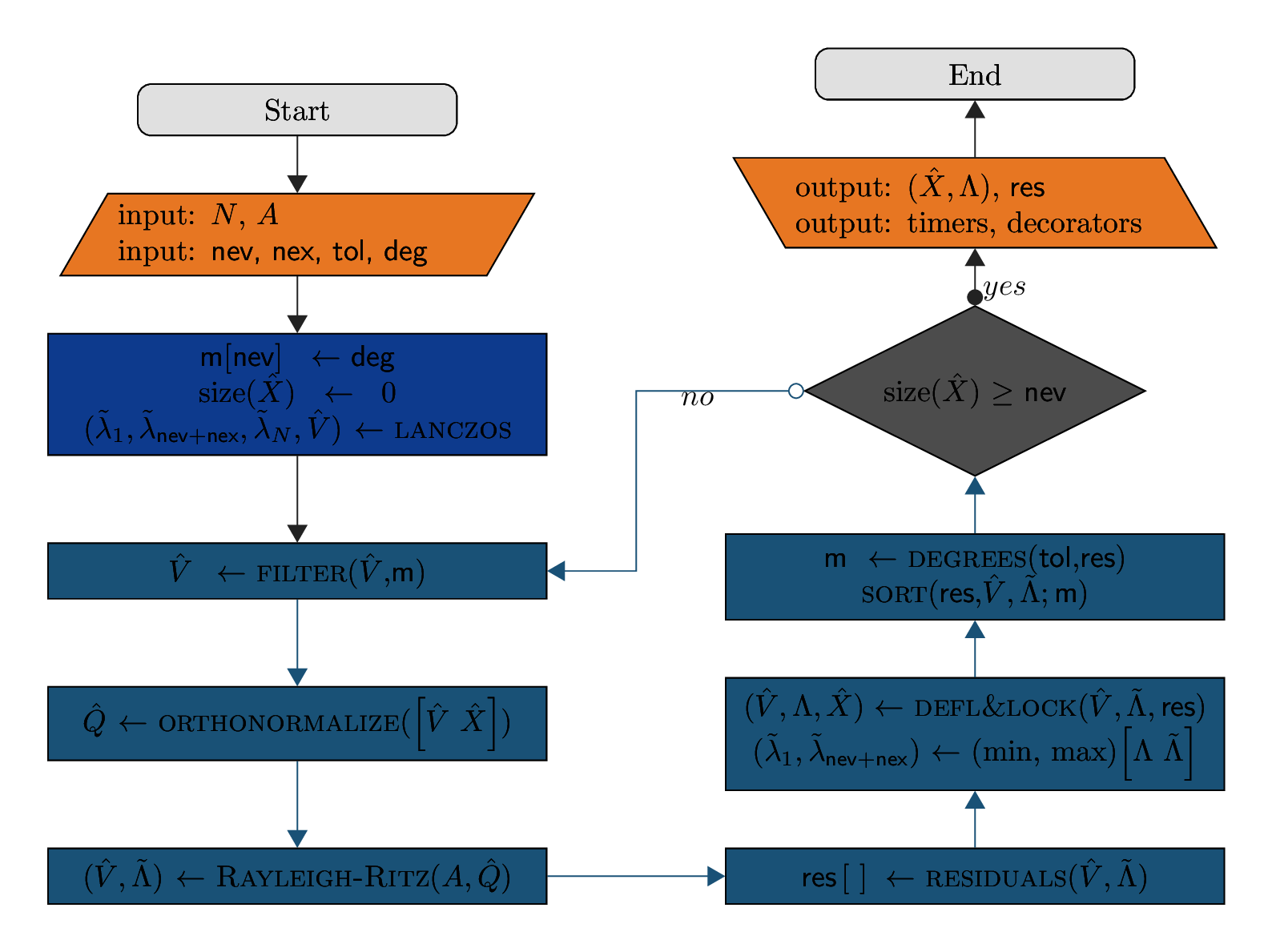
_images/ChASE_flowchart.png

\(A, N\)

The Hermitian matrix and corresponding rank.

nev,nex

Number of desired eigenpairs, Extra size of search space

tol,deg

Threshold of residual’s tolerance, initial degree of Chebyshev polynomials

\(\hat{V},\hat{Q},\hat{X}\)

Matrix of vectors: filtered, orthonormalized, deflated and locked

\(\tilde{\Lambda},\Lambda\)

Matrix of eigenvalues: computed, deflated and locked

\(m[],\textsf{res}[]\)

Vectors: optimized degrees, eigenpairs residuals

FILTER

Chebyshev polynomial filter aligning \(\hat{V}\) to the desired eigenspace

ORTHONORMALIZE

QR factorization orthogonalizing filtered vectors together with deflated ones

RAYLEIGH-RITZ

Projection of \(A\) into search space defined by \(\hat{Q}\) and diagonalization of reduced problem

DEFL&LOCK

Deflation and locking of eigenpairs whose residuals are below the tolerance threshold

DEGREES

Computation of optimal polynomial degree for each vector in \(\hat{V}\)

Use Case and Features

  • Real and Complex: ChASE is templated for real and complex numbers. So it can be used to solve real symmetric eigenproblems as well as complex Hermitian ones.

  • Eigespectrum: ChASE algorithm is designed to solve for the extremal portion of the eigenspectrum (i.e., \(\{\lambda_1, \dots ,\lambda_\textsf{nev}\}\)). By default it computes the lowest portion of the spectrum but it can compute as well the largest portion by solving for \(-A\). The library is particularly efficient when no more than 20% of the extremal portion of the eigenspectrum is sought after. For larger fractions the subspace iteration algorithm may struggle to be competitive. Converge could become an issue for fractions close to or larger than 50%.

  • Type of Problem: ChASE can currently handle only standard eigenvalue problems. Generalized eigenvalue problems of the form \(A\hat{x} = \lambda B \hat{x}\), with \(B\) s.p.d., can be solved after factorizing \(B = L L^T\) and transforming the problem into standard form \(A = L^{-1} A L^{-T}\).

  • Sequences: ChASE is particularly efficient when dealing with sequences of eigenvalue problems, where the eigenvectors solving for one problem can be use as input to accelerate the solution of the next one.

  • Vectors input: Since it is based on subspace iteration, ChASE can receive as input a matrix of vector \(\hat{V}\) equal to the number of desired eigenvalues. ChASE can experience substantial speed-ups when \(\hat{V}\) contains some information about the sought after eigenvectors.

  • Degree optimization: For a fixed accuracy level, ChASE can optimize the degree of the Chebyshev polynomial filter so as to minimize the number of FLOPs necessary to reach convergence.

  • Precision: ChASE is also templated to work in Single Precision (SP) or Double Precision (DP).