Versions of the library

ChASE is a modern C++ library for solving dense eigenvalue problems. The library provides multiple implementation variants to support different computing architectures and problem types. ChASE can be installed with minimal dependencies (BLAS, LAPACK) for sequential execution, or with MPI/ScaLAPACK for parallel execution on distributed systems.

Implementation Variants

ChASE provides four main implementation classes, each optimized for different computing environments:

Sequential Implementations

ChASECPU (chase::Impl::ChASECPU): Sequential CPU implementation for single-node execution. This is the simplest configuration, suitable for single CPU systems or shared-memory multi-core systems. It uses BLAS and LAPACK for all numerical operations and supports both Hermitian and pseudo-Hermitian (Quasi-Hermitian) matrices.

ChASEGPU (chase::Impl::ChASEGPU): Sequential GPU implementation for single-node execution with GPU acceleration. This configuration offloads computations to GPU using CUDA, cuBLAS, and cuSOLVER libraries. Ideal for systems with one or more GPU cards, supporting both Hermitian and pseudo-Hermitian matrices.

Parallel Implementations

pChASECPU (chase::Impl::pChASECPU): Parallel CPU implementation using MPI for distributed-memory systems. This configuration is best suited for multi-node CPU clusters. It uses ScaLAPACK for distributed linear algebra operations and supports multiple matrix distribution schemes (Block, Block-Cyclic). Typically used with one MPI rank per NUMA domain and OpenMP threads for intra-node parallelism.

pChASEGPU (chase::Impl::pChASEGPU): Parallel GPU implementation using MPI or NCCL for distributed-memory systems with GPU acceleration. This configuration supports both MPI (with CUDA-aware MPI) and NCCL backends for inter-node GPU communication. Currently supports one GPU card per MPI rank. Ideal for heterogeneous computing clusters with multiple GPU nodes.

Matrix Types

ChASE supports two types of eigenvalue problems (Hermitian and Pseudo-Hermitian), each available in both sequential (non-distributed) and parallel (distributed) variants. The choice of matrix type depends on whether you are using sequential or parallel implementations.

Sequential (Non-Distributed) Matrix Types

These matrix types are used with sequential implementations (ChASECPU and ChASEGPU):

Hermitian (Symmetric) Matrices

Matrix Type: chase::matrix::Matrix<T> (CPU) or chase::matrix::Matrix<T, chase::platform::GPU> (GPU)

Problem Form: \(A \hat{x} = \lambda \hat{x}\) where \(A = A^*\)

Rayleigh-Ritz: Standard projection (NORMAL-RAYLEIGH-RITZ)

Orthonormalization: Standard QR factorization

Pseudo-Hermitian (Quasi-Hermitian) Matrices

Matrix Type: chase::matrix::QuasiHermitianMatrix<T> (CPU) or chase::matrix::QuasiHermitianMatrix<T, chase::platform::GPU> (GPU)

Problem Form: BSE Hamiltonian \(H\) satisfying \(SH = H^*S\)

Rayleigh-Ritz: Oblique projection with S-metric (OBLIQUE-RAYLEIGH-RITZ)

Orthonormalization: S-orthonormal QR factorization

Use Case: Bethe-Salpeter Equation (BSE) and similar applications

Parallel (Distributed) Matrix Types

These matrix types are used with parallel implementations (pChASECPU and pChASEGPU) and support different distribution schemes across MPI processes:

Hermitian (Symmetric) Matrices

Block Distribution: chase::distMatrix::BlockBlockMatrix<T, Platform>

Block-Cyclic Distribution: chase::distMatrix::BlockCyclicMatrix<T, Platform>

Redundant Distribution: chase::distMatrix::RedundantMatrix<T, Platform>

Problem Form: \(A \hat{x} = \lambda \hat{x}\) where \(A = A^*\)

Rayleigh-Ritz: Standard projection (NORMAL-RAYLEIGH-RITZ)

Orthonormalization: Standard QR factorization

Platform: Can be chase::platform::CPU or chase::platform::GPU

Pseudo-Hermitian (Quasi-Hermitian) Matrices

Block Distribution: chase::distMatrix::QuasiHermitianBlockBlockMatrix<T, Platform>

Block-Cyclic Distribution: chase::distMatrix::QuasiHermitianBlockCyclicMatrix<T, Platform>

Problem Form: BSE Hamiltonian \(H\) satisfying \(SH = H^*S\)

Rayleigh-Ritz: Oblique projection with S-metric (OBLIQUE-RAYLEIGH-RITZ)

Orthonormalization: S-orthonormal QR factorization

Use Case: Bethe-Salpeter Equation (BSE) and similar applications

Platform: Can be chase::platform::CPU or chase::platform::GPU

Matrix Distributions (Parallel Implementations)

For parallel implementations (pChASECPU and pChASEGPU), ChASE organizes MPI processes in a 2D grid and supports multiple data distribution schemes for assigning sub-blocks of the dense matrix to different MPI ranks.

Block Distribution

The Block Distribution (chase::distMatrix::BlockBlockMatrix) assigns each MPI rank of the 2D grid a contiguous block of the dense matrix. This distribution scheme is optimal for the Hermitian Matrix-Matrix Multiplication kernel, which is the most computationally intensive operation in ChASE. The block distribution results in large, contiguous matrix-matrix multiplications on each node, often achieving performance close to the hardware theoretical peak. Additionally, this data distribution allows efficient offloading of computations to GPU accelerators.

\[\begin{split}A=\left(\begin{array}{c|c|c} A_{0,0} & A_{0,1} & A_{0,2} \\ \hline A_{1,0} & A_{1,1} & A_{1,2} \\ \hline A_{2,0} & A_{2,1} & A_{2,2} \end{array}\right)\end{split}\]

The figure above shows an example of ChASE distributing a \(n \times n\) dense matrix \(A\) into a \(3 \times 3\) grid of MPI processes. In this example, the matrix \(A\) is split into a 2D grid of sub-matrices \(A_{i,j}\) where \(i \in [0,2]\) and \(j \in [0,2]\). Each sub-matrix \(A_{i,j}\) is assigned to the corresponding MPI rank in the 2D process grid.

Block-Cyclic Distribution

The Block-Cyclic Distribution (chase::distMatrix::BlockCyclicMatrix) is a 2D block-cyclic distribution scheme originally introduced for dense matrix computations on distributed-memory machines. Compared to the Block Distribution, the main advantage of the Block-Cyclic Distribution is improved load balance for matrix operations where the computational work varies across different matrix entries, such as QR and LU factorizations.

Even though load balance is typically not a problem for ChASE (since the Hermitian Matrix-Matrix Multiplication kernel is well-balanced with Block Distribution), ChASE still provides the Block-Cyclic Distribution as an option to avoid data redistribution between different distribution schemes, which may be required for some applications, e.g., solving generalized eigenproblems with Cholesky factorization. In ChASE, the implementation with Block-Cyclic Distribution can achieve similar performance as the implementation with Block Distribution.

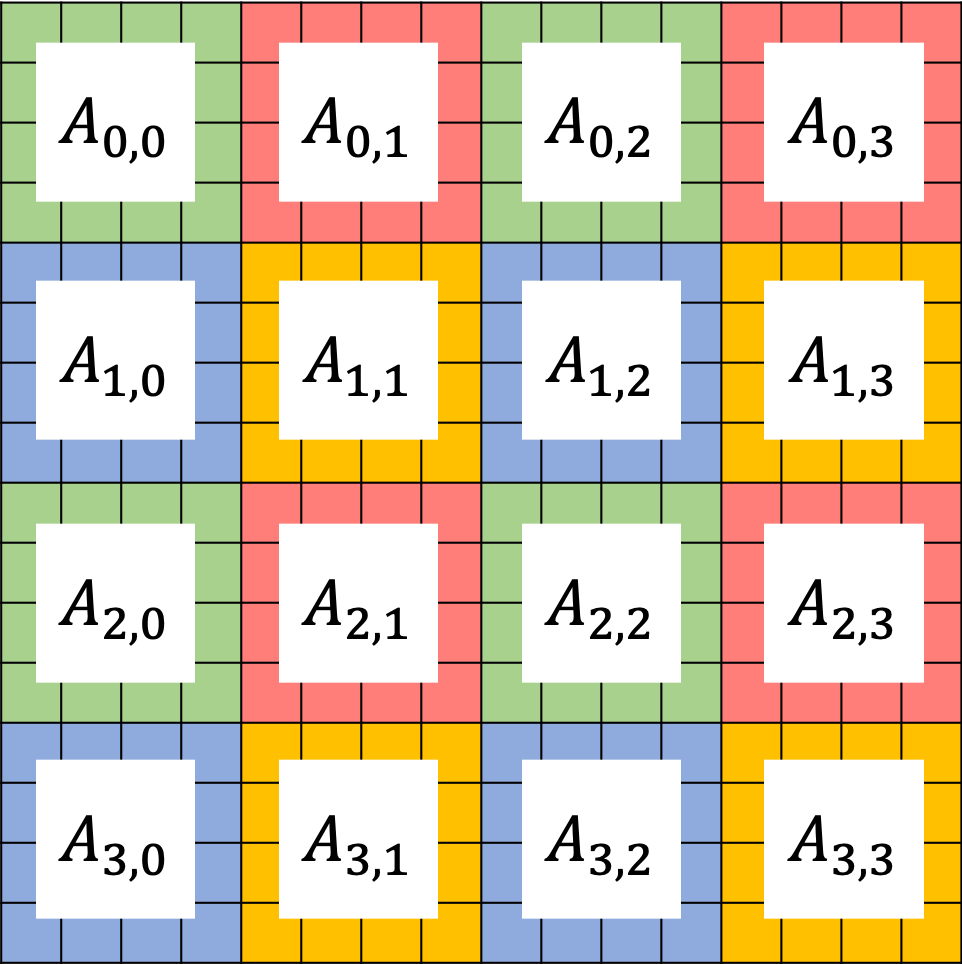
The figure above shows an example of ChASE distributing a \(n \times n\) dense matrix \(A\) into a \(2 \times 2\) grid of MPI processes in a block-cyclic scheme. Denoting the 4 MPI processes as \(P_{0,0}\), \(P_{0,1}\), \(P_{1,0}\), and \(P_{1,1}\), they are marked as green, red, blue and yellow, respectively in the figure above. In this example, the matrix \(A\) is split into a 2D grid of sub-matrices \(A_{i,j}\) where \(i \in [0,3]\) and \(j \in [0,3]\). Each sub-matrix is assigned to one MPI process in a round-robin manner so that each MPI rank receives several non-adjacent blocks, improving load balance for certain operations.

For more details about Block-Cyclic Distribution, please refer to the Netlib ScaLAPACK documentation.

Redundant Distribution

The Redundant Distribution (chase::distMatrix::RedundantMatrix) stores a complete copy of the matrix on each MPI rank. This distribution is useful for small to medium-sized matrices where communication overhead would be prohibitive, or for operations that require global access to the matrix data.

Backend Communication

For parallel GPU implementations, ChASE supports multiple communication backends:

MPI Backend (chase::grid::backend::MPI): Standard MPI communication, with support for CUDA-aware MPI when available. This backend is suitable for systems with standard MPI installations and provides good performance for inter-node communication.

NCCL Backend (chase::grid::backend::NCCL): NVIDIA Collective Communications Library for optimized GPU-to-GPU communication. This backend provides superior performance for multi-GPU systems, especially on systems with high-speed interconnects like NVLink or InfiniBand.